Hash Table

정의

• 해시 테이블이란 해시 함수를 사용해서 변환한 값을 index로 삼아 key와 value를 저장하는 자료구조다.
• 해시 테이블은 어떤 특정 값을 받아서 해시 함수에 입력하고, 함수의 출력값을 인덱스로 삼아 데이터를 저장한다.
• 즉 해시 함수를 이용해서 key를 hash value로 매핑하고, 이 hash value를 index로 삼아 데이터의 value를 buckets(혹은 slots)에 저장한다.
• 파이썬의 dictionary, 루비의 hash, 자바의 map이 해시 테이블의 대표적인 예다.

특징

• 기본 연산으로는 search, insert, delete가 있다.
• 순차적으로 데이터를 저장하지 않는다.
• key를 통해서 value를 얻을 수 있다. => 이진 탐색 트리나 배열에 비해서 속도가 획기적으로 빠름
• 커다란 데이터를 해시해서 짧은 길이로 축약할 수 있기 때문에 데이터를 비교할 때 효율적이다.
• value는 중복 가능하지만 key는 유니크해야 한다.
• 수정 가능하다(mutable)
• 보통 배열로 미리 hash table 사이즈만큼 생성 후에 사용한다.

해시 테이블은 key-value가 1:1 매핑되어 있기 때문에 검색, 삽입, 삭제 과정에서 모두 평균적으로 O(1)의 시간복잡도를 갖는다. 공간 복잡도는 O(N)인데 여기서 N은 키의 개수다.

Hash table time complexity in Big O notation
Algorithm	Average	Worst case
space	O(n)	O(n)
search	O(1)	O(n)
insert	O(1)	O(n)
delete	O(1)	O(n)

해시 함수

해시

해시란 단방향 암호화 기법으로 해시 함수를 이용하여 고정된 길이의 암호화된 문자열로 바꿔버리는 것을 의미한다. 이때 매핑 전 원래 데이터의 값을 key, 매핑 후 데이터 값을 hash value, 매핑하는 과정을 hashing이라고 한다.

그렇다면 해시 함수는 어떻게 작성할 수 있을까?

해시 함수

• 임의의 길이를 갖는 메시지를 입력받아서 고정된 길이의 해시값을 출력하는 함수
• 어떤 입력 값에도 항상 고정된 길이(해시 함수에 따라 비슷한 길이까지 포함)의 해시값을 출력한다.
• 해시 함수를 통해 입력값은 완전히 새로운 모습의 데이터로 만들어지기 때문에 암호화 영역에서 아주 주요하게 사용되고 있다. SHA(Secure Hash Algorithm)알고리즘이 그 대표적인 예시다.
• 입력 값의 일부가 변경되면 전혀 다른 값을 출력하는데 이것을 가리켜 눈사태 효과라고 한다. 이 눈사태 효과로 결과값으로는 입력값을 유추할 수가 없다. 역추적이 안된다는 말은 단방향으로만 되어 있다는 의미를 내포한다.

단점: 해시 충돌

하지만 이 해시 함수에도 단점이 존재하는데, 해시 함수는 입력값의 길이가 어떻든 고정된 길이의 값을 출력하기 때문에 입력값이 다르더라도 같은 결과값이 나오는 경우가 있다.

이것을 해시 충돌 hash collision이라고 표현하며, 충돌이 적은 해시 함수가 좋은 해시함수다.

해시 충돌

다음 그림(출처 (opens new window))을 보자. ARGOS와 MINIBEEF가 같은 해시 값을 가지며 충돌이 발생했다.

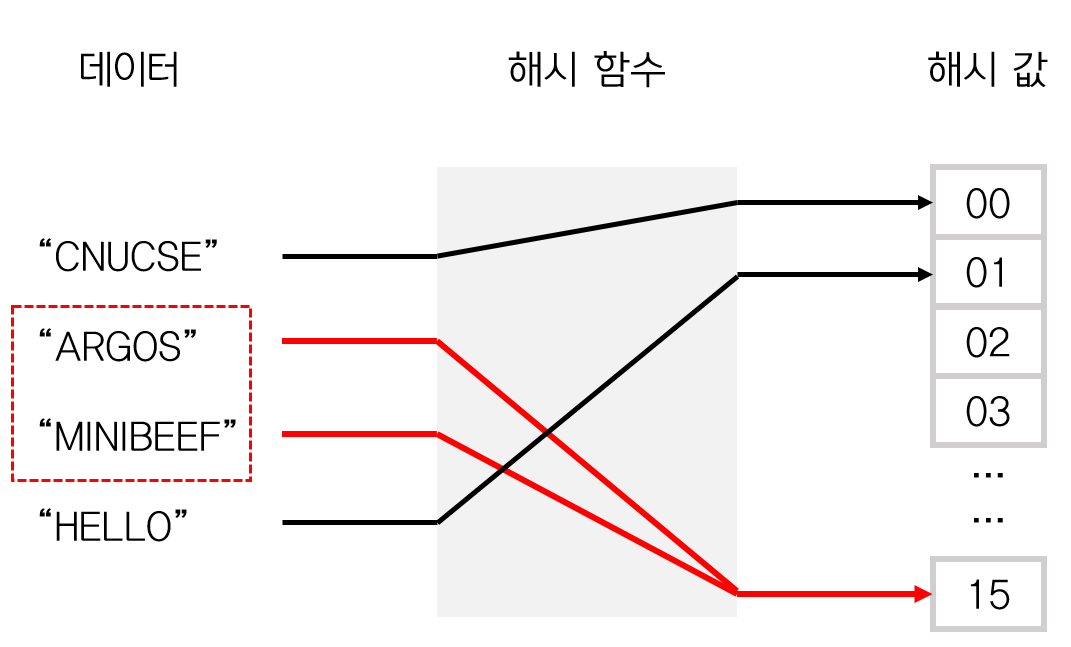
해시 충돌을 설명하기 위해서는 적재율(load factor)이라는 개념이 필요하다. 적재율이란 해시 테이블의 크기에 대한 키의 개수의 비율을 뜻한다. 즉 키의 개수를 K, 해시 테이블의 크기를 N이라고 했을 때 적재율은 K/N이다. 만약 충돌이 발생하지 않을 경우 해시 테이블의 탐색, 삽입, 삭제 연산은 모두 O(1)에 실행되지만, 충돌이 발생할 경우에는 탐색과 삭제 연산이 O(K)만큼 걸리게 된다.

해시 충돌이 1도 없는 해시 함수를 만드는 것은 불가능하다. 따라서 해시 충돌에 대해 안전하다는 해시 함수는 '충돌을 찾는 게 거~의 희박하다'라는 뜻이다. 이 해시 충돌이 발생하는 근본적인 원인은 비둘기집 원리 (opens new window)다. 즉 해시 함수가 무한한 가짓수의 입력값을 받아 유한한 가짓수의 출력값을 생성하는 경우에는 비둘기집 원리에 의해 해시 충돌은 항상 존재한다. 띠라서 해시 테이블의 충돌을 완화하는 방향으로 문제를 보완해야 한다.

해시 충돌 완화

해시 충돌을 완화하는 데는 다양한 방법이 있다.

• 개방 주소법 open addressing으로 해시 테이블 크기는 고정하면서 저장할 위치를 잘 찾거나,
• 분리 연결법 seperate chaining으로 해시 테이블의 크기를 유연하게 만드는 방법이 대표적이다.

아래 이미지(출처) (opens new window)를 보면서 어떤 개념인지 살펴보자.

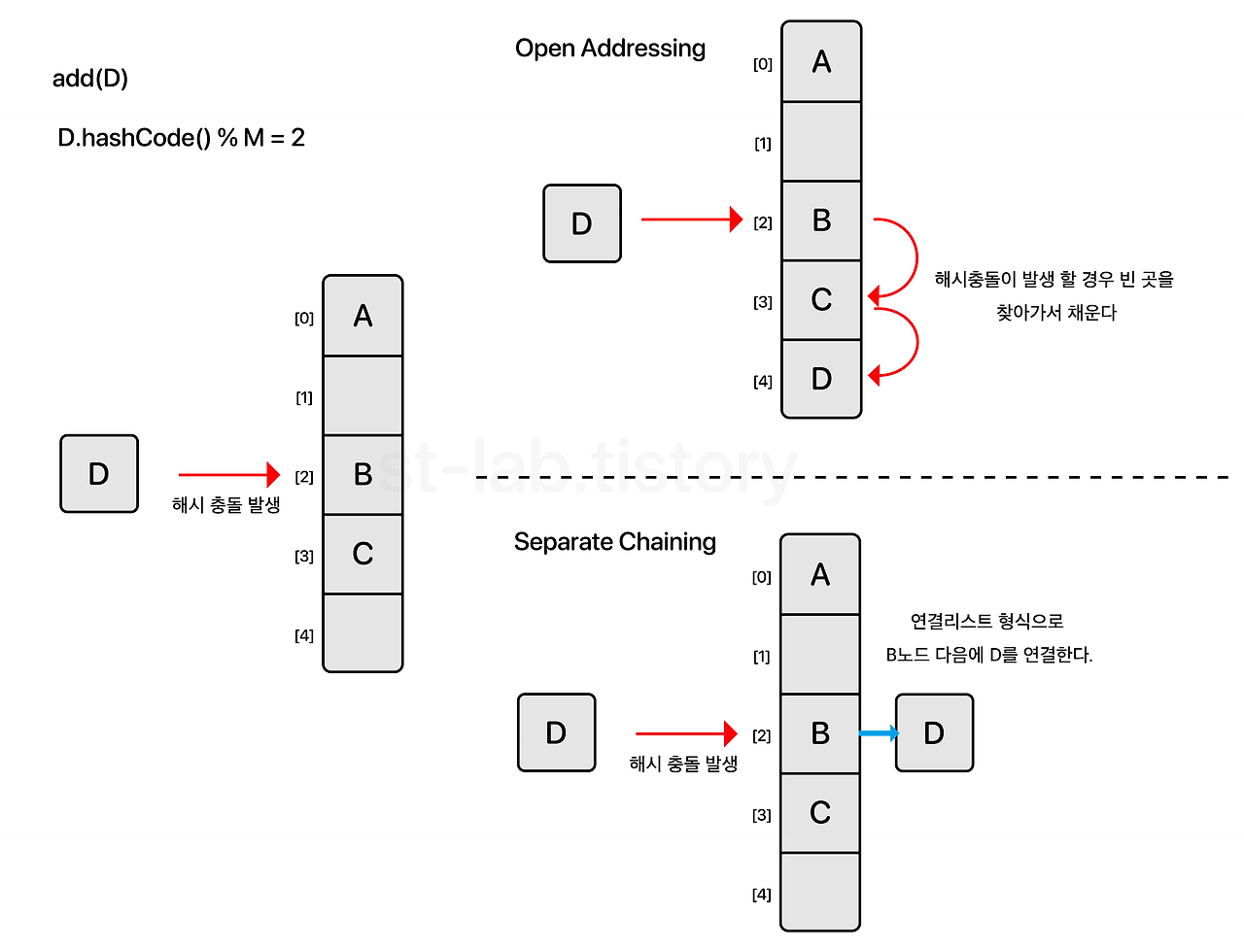
1. 개방 주소법 open address

open addressing은 한 버킷 당 들어갈 수 있는 엔트리는 하나이지만 해시 함수로 얻은 주소가 아닌, 다른 주소에 데이터를 저장할 수 있도록 허용하는 방법이다. 하지만 이 방법은 부하율(load factor)이 높을 수록(= 테이블에 저장된 데이터의 밀도가 높을수록) 성능이 급격히 저하된다. 개방 주소법의 주요 목적은 저장할 엔트리를 위한 다음의 slot을 찾는 것인데 이 방법으로 2가지가 널리 쓰인다. - 이미지 출처 (opens new window)

(1) 선형 탐사법 Linear Probing

말 그대로 가장 간단하게 선형으로 순차적 검색을 하는 방법이다. 해시 함수로 나온 해시 index에 이미 다른 값이 저장되어 있다면, 해당 해시값에서 고정 폭을 옮겨 다음 해시값에 해당하는 버킷에 액세스한다. 여기에 또 다른 데이터가 있다면 또 다시 고정폭으로 이동해 액세스한다.

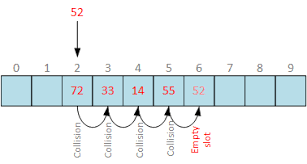
이 경우에는 특정 해시 값의 주변이 모두 채워져 있는 일차 군집화(primary clustering) 문제에 취약하다. 예를 들어 모든 키가 100이라는 해시값으로 매핑이 될 경우 충돌을 100%가 된다. 따라서 해시 충돌이 해시 값 전체에 균등하게 발생할 때 유용한 방법이다.

(2) 제곱 탐사법 Quadratic Probing

선형 탐사법과 동일한데, 고정폭이 아니라 제곱으로 늘어난다. 따라서 2^1, 2^2, 2^3로 이동해서 데이터를 할당한다.

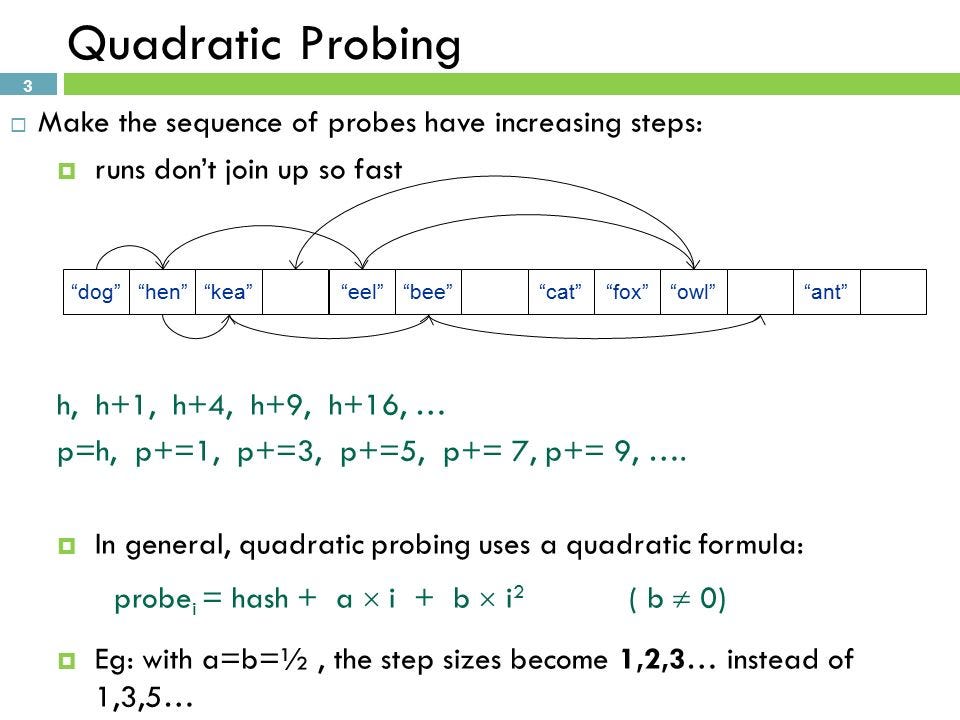
따라서 제곱 탐사법을 이용한 경우 데이터의 밀집도가 선형 탐사법보다 낮기 때문에 다른 해시값까지 영향을 받아서 연쇄적으로 충돌이 발생할 가능성이 적다. 하지만 선형 탐사법보다는 캐시의 성능이 떨어져서 속도의 문제가 발생한다.

(3) 이중 해싱 Double Hashing

이 외에도 이중 해싱(double hashing) 방법이 있다. 이 방법은 탐사할 해시값의 규칙값을 없애서 클러스터링을 방지한다. 즉 해시 함수를 이중으로 사용하는데, 하나는 최초의 해시값을 얻을 때, 다른 하나는 해시 충돌이 일어났을 때 탐사 이동폭을 얻기 위해 사용한다. 이렇게 되면 최초 해시값이 같더라도 탐사 이동폭이 달라지고, 탐사 이동폭이 같더라도 최초 해시값이 달라져 위의 두 방법을 모두 완화할 수 있다.

2. 분리 연결법 seperate chaining

분리 연결법은 개방 주소법과는 달리 한 버킷(슬롯) 당 들어갈 수 있는 엔트리의 수에 제한을 두지 않는다. 이때 버킷에는 링크드 리스트 linked list나 트리 tree를 사용한다.

해시 충돌이 일어나더라도 linked list로 노드가 연결되기 때문에 index가 변하지 않고 데이터 개수의 제약이 없다는 장점이 있다. 하지만 메모리 문제를 야기할 수 있으며, 테이블의 부하율에 따라 선형적으로 성능이 저하된다. 따라서 부하율이 작을 경우에는 open addressing 방식이 빠르다.

위의 2가지 방법 이외에도 해시 테이블의 적재율이 높아진 경우에는 크기가 더 큰 새로운 테이블을 만들어서 기존 데이터를 옮겨서 사용하는 방법이 있다. 혹은 분리 연결법을 사용했을 경우엔 재해싱을 통해서 너무 길어진 리스트의 길이를 나누어서 다시 저장할 수도 있다. 그리고 마지막으로 해시 함수 자체를 올바르게 쓰는 방법이다. 특정 값에 치우치지 않고 해시값을 고르게 만들어내는 좋은 해시 함수를 사용하는 것이다.

자바스크립트의 object는 해시 테이블일까?

자바스크립트에도 이 해시테이블과 비슷한 것을 찾을 수 있다.

바로 object다. key-value 값으로 이뤄져 있고 key는 유니크해서 key를 index 삼아 value를 찾을 수 있고, 데이터의 삭제가 가능한 그것..

실제로 많은 글을 읽다보면 해시 테이블을 자바스크립트의 객체와 같다고 설명한다. (eg. dictionaries in Python, Hashes in Ruby, Maps in Java, Objects in JavaScript)

하지만 정확히 자바스크립트 객체는 해시 테이블이 아니다. V8 엔진을 포함한 대부분의 자바스크립트 엔진은 해시 테이블과 유사하지만 높은 성능을 위해 일반적인 해시 테이블보다 나은 방법으로 객체를 구현한다. (V8 블로그 참고 (opens new window))

자바, C++ 같은 클래스 기반 객체지향 프로그래밍 언어는 사전에 정의된 클래스를 기반으로 객체(인스턴스)를 생성한다. 다시 말해, 객체를 생성하기 이전에 이미 프로퍼티와 메서드가 정해져 있으며 그대로 객체를 생성한다. 객체가 생성된 이후에는 프로퍼티를 삭제하거나 추가할 수 없다.
하지만 자바스크립트는 클래스 없이 객체를 생성할 수 있으며 객체가 생성된 이후라도 동적으로 프로퍼티와 메서드를 추가할 수 있다. 이는 사용하기 매우 편리하지만 성능 면에서는 이론적으로 클래스 기반 객체지향 프로그래밍 언어의 객체보다 생성과 프로퍼티 접근에 비용이 더 많이 드는 비효율적인 방식이다. 따라서 V8 자바스크립트 엔진에서는 프로퍼티에 접근하기 위해 동적 탐색(dynamic lookup) 대신 히든 클래스(hidden class)라는 방식을 사용해 C++ 객체의 프로퍼티에 접근하는 정도의 성능을 보장한다. 히든 클래스는 자바와 같이 고정된 객체 레이아웃(클래스)과 유사하게 동작한다.

- 이웅모, 자바스크립트 Deep Dive

따라서 자바스크립트의 Object는 key-value의 집합으로 해시 테이블과 유사해보이지만, 자바스크립트 엔진이 object를 해시 테이블의 원리로 실행하지 않기 때문에 해시 테이블이 아니다.

그렇다면 Map, Set, WeakMap, WeakSet은 해시 테이블일까?

또 자바스크립트에서 해시 테이블과 유사한 것으로 언급되는 대상은 Map, Set, WeakMap, WeakSet이다. 실제 ECMAScript에서도 위의 4가지를 설명하며 hash tables를 언급한다. (링크 (opens new window))

Maps must be implemented using either hash tables or other mechanisms that, on average, provide access times that are sublinear on the number of elements in the collection. The data structure used in this specification is only intended to describe the required observable semantics of Maps. It is not intended to be a viable implementation model.

결국 이 모든 data structure들은 크롬의 V8 엔진, 사파리의 니트로, 파이어폭스의 스파이더몽키, 엣지의 차크라 등등.. 자바스크립트를 컴파일하고 실행하는 엔진이 이 데이터 구조들을 어떻게 구현했느냐에 달려있다.

따라서 '자바스크립트의 해시 테이블은 Map, Set이 있어요~'라는 말은 단순히 V8의 Set과 Map의 get, set, add, has의 시간 복잡도가 O(1)이기 때문에 비슷하다고 여겨지는 것일 뿐, 원리는 해시 테이블로 구현되지 않았다는 걸 알아두자.

그렇다면 해시 테이블의 대안으로 Object와 Map 중에 무엇을 고를까?

만약 해시 테이블의 대용으로 object와 Map 중에 고르라면.. 무엇을 사용하면 될까? MDN에 따르면 데이터 크기가 크거나, entry들을 추가하거나 삭제하는 빈도가 더 높을 수록 object보다 Map을 사용하는 것이 좋다. 위의 상황에서는 object보다 Map이 더 나은 성능을 보이기 때문이다.

그리고 data의 사이즈를 알고 싶을 때 object는 Object.values(obj).length로 접근해서 O(n)이 걸리는데, Map은 map.size로 접근해서 object보다 더 빠르다. (cf. the average duration of size determination of a map with 10 million entries: Plain js object => Max 1.6sec, Map => < 1ms)

이외에도.. Map은 직접 iteration이 가능하다는 점, key order를 갖는다는 점 등등으로 Map을 사용하면 얻을 수 있는 이점이 많다. 다만.... 이 모든 이점에도 불구하고 object를 사용하는 이유는 데이터를 구현하기 간단하기 때문일 것. (모두 다 알 거라고 생각한다. 언제 get() 써가며 값 넣을거야)

자바스크립트로 해시 테이블 구현하기

class HashTable {
  constructor(size) {
    this.data = new Array(size);
  }

  // Hash Function
  _hash(key) {
    let hash = 0;
    for (let i = 0; i < key.length; i++) {
      hash = (hash + key.charCodeAt(i) * i) % this.data.length;
    }

    return hash;
  }

  /**
   * Insert a key-pair value in object.
   * @param {key} key
   * @param {value} value
   * @return {object} this.data
   */
  set(key, value) {
    const address = this._hash(key);

    if (!this.data[address]) {
      this.data[address] = [];
    }

    // If there is already a data in the address, push it in the same array.
    // This will happen in case of hash collision (enough data, less memory space).
    this.data[address].push([key, value]); // Time complexity = O(1)
    return this.data;
  }

  /**
   * Look for a value at given key.
   * @param {key} key
   * @return {any} value
   */
  get(key) {
    const address = this._hash(key);
    const currentBucket = this.data[address];

    // In case of hash collision this will have length more than 1.
    if (currentBucket) {
      // Time Complexity = O(1) most often. In worst case (hash collision) it will be O(n)
      for (let i = 0; i < currentBucket.length; i++) {
        if (currentBucket[i][0] === key) {
          return currentBucket[i][1];
        }
      }
    }
  }

  /**
   * Find all keys in the object.
   * Time Complexity = O(N),
   * in case of hash collision it will be O(N^2) where N is keys.
   * @return {object} keysArray
   */
  keys() {
    let keysArray = [];

    for (let i = 0; i < this.data.length; i++) {
      if (this.data[i] && this.data[i].length) {
        if (this.data[i].length > 1) {
          for (let j = 0; j < this.data[i].length; j++) {
            if (this.data[i][j]) {
              keysArray.push(this.data[i][j][0]);
            }
          }
        } else {
          keysArray.push(this.data[i][0][0]);
        }
      }
    }

    return keysArray;
  }
}

const myHashTable = new HashTable(50);
myHashTable.set('has_garden', true);
console.log(myHashTable.get('has_garden'));

myHashTable.set('house_number', 54);
console.log(myHashTable.get('house_number'));

myHashTable.set('street_name', 'Main Street');
console.log(myHashTable.get('street_name'));

console.log(myHashTable.keys());

(출처 (opens new window)에서 확인해볼 수 있다..)

이상 자료구조의 해시 테이블을 정리해보았다!

참고자료

• DS With JS — Hash Tables (opens new window)
• 해싱, 해시함수, 해시테이블 (opens new window)
• JavaScript Hash Table – Associative Array Hashing in JS (opens new window)
• 해쉬 알고리즘 요약 정리, 테스트 코드 (opens new window)
• JavaScript와 함께 해시테이블을 파헤쳐보자 (opens new window)
• 해시함수란 무엇인가? (opens new window)
• Stop Using Objects as Hash Maps in JavaScript (opens new window)
• DS 해쉬 테이블(Hash Table)이란? (opens new window)
• 해시 충돌 (opens new window)
• 자바 - 해시 셋 구현하기 (opens new window)
• Open Addressing: Resolving Collisions One Day At A Time! (opens new window)
• ES6 — Map vs Object — What and when? (opens new window)